(This post is an experiment in two senses. First, to test embedding graphs from the Desmos calculator into the post. Second, to show the results of a mathematical experiment carried out on Desmos and Twitter last night.)
In Spivak’s classic textbook Calculus, one exercise asks the reader to show that each of the following (complex) power series has radius of convergence 1: \[ \sum_{n=1}^{\infty} \frac{z^n}{n^2}, \hspace{0.5in} \sum_{n=1}^{\infty} \frac{z^n}{n}, \hspace{0.5in} \sum_{n=1}^{\infty} z^n. \] (I’ll leave that task to you. Hint: ratio test.) Another exercise then says, “Prove that the first series converges everywhere on the unit circle; that the third series converges nowhere on the unit circle; and that the second series converges for at least one point on the unit circle and diverges for at least one point on the unit circle.” Points where a series converges always raise a new problem: can we tell what value it converges to? Generally, that problem is hard. But at a point where a series is known to diverge, the story’s over, right? Well, no. There are many ways for a series to diverge.
I want to focus here on the behavior of $\sum z^n$ when $|z| = 1$. The series diverges, of course, because the size of every term is 1. But what do the partial sums look like? What do their real and imaginary parts look like? My thoughts on this began last night when I plotted the graph of $\sum_{n=1}^{50} \sin nx$:
(Click on the graph to go to an interactive version.) To my surprise, there appeared to be well-defined curves bounding the top and bottom of this graph. To be more precise, the points corresponding to critical values (or local extreme values) of the function lie on a pair of analytic curves. After some playing around, I found these curves to be the graphs of ${-\frac{1}{2}} \tan \frac{x}{4}$ and $\frac{1}{2} \cot \frac{x}{4}$ (shown in blue and green, respectively, below).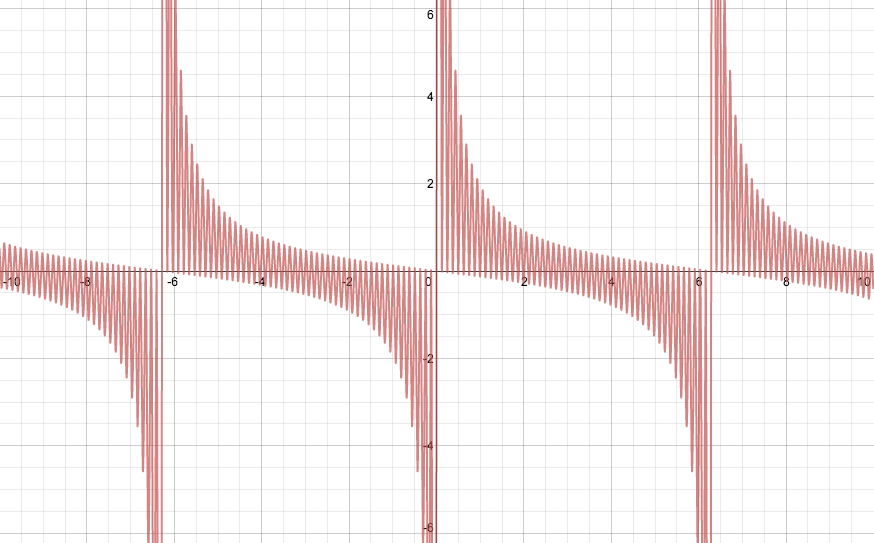
I sent out a tweet about my discovery: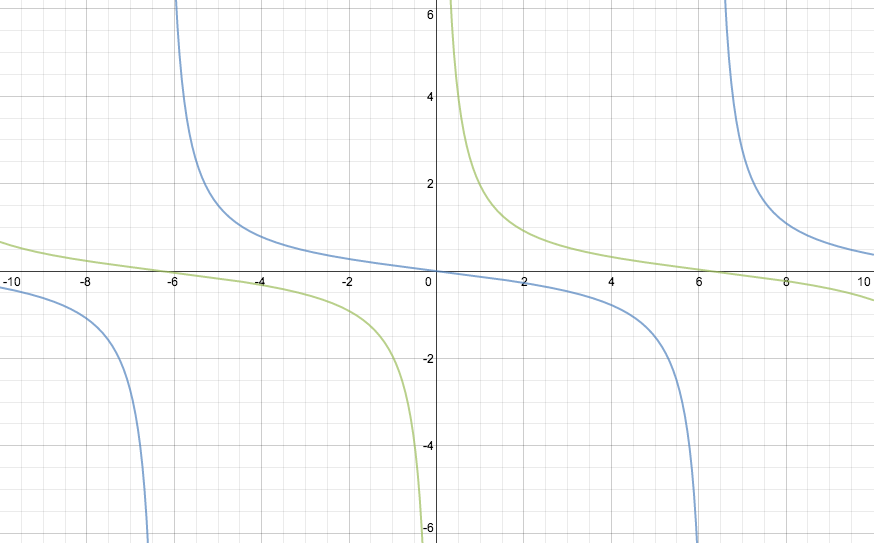
I went investigating and found some hints that this behavior might be related to the Fourier series of the cotangent. Meanwhile, my tweet generated some interest, including this response:This certainly *looks* like it fits, but I have no idea why. desmos.com/calculator/e67… @desmos #math #mathchat
— Joshua Bowman (@Thalesdisciple) June 11, 2013
Also, later in the evening, Desmos took my initial graph and augmented it:@thalesdisciple @desmos Looks like using formula for a partial geometric sum on e^(inx) should explain it?Thanks for posting.Very cool.
— Paul Johnson (@ptwiddle) June 11, 2013
Paul’s on the right track, which brings us back to the Spivak exercise I mentioned earlier.@ptwiddle @thalesdisciple What a fun exploration! I added a few things to your original graph. desmos.com/calculator/wz2… #SinesOfMadness
— Desmos.com (@Desmos) June 12, 2013
To get a point of the unit circle, write $z = \mathrm{e}^{ix}$, with $x \in \mathbb{R}$. Then the summation formula for partial geometric series yields \[ 1 + \mathrm{e}^{ix} + \cdots + \mathrm{e}^{imx} = \frac{1 - \mathrm{e}^{i(m+1)x}}{1 - \mathrm{e}^{ix}}. \] We can take imaginary parts of both sides and use some trig identities to get \[ \sin x + \cdots + \sin mx = \frac{\cos \frac{x}{2} - \cos \big(m+\frac{1}{2}\big)x}{2 \sin \frac{x}{2}}. \] (Note that Desmos included this latter formula in their augmented form of the graph. See also this nice derivation.) On the other hand, the tangent half-angle formulas give us \[ -\tan \frac{x}{4} = \frac{\cos \frac{x}{2} - 1}{\sin \frac{x}{2}} \qquad\text{and}\qquad \cot \frac{x}{4} = \frac{\cos \frac{x}{2} + 1}{\sin \frac{x}{2}}. \] When $\sin\frac{x}{2}$ is positive (for example, when $0 < x < 2\pi$), we have \[ -\frac{1}{2} \tan \frac{x}{4} \le \sin x + \cdots + \sin mx \le \frac{1}{2} \cot \frac{x}{4}, \] with equality on the left whenever $\cos\big(m+\frac{1}{2}\big)x = 1$ and equality on the right whenever $\cos\big(m+\frac{1}{2}\big)x = -1$. The direction of the inequalities is reversed when $\sin\frac{x}{2} < 0$, but the rest of the analysis remains the same. This is the desired result.
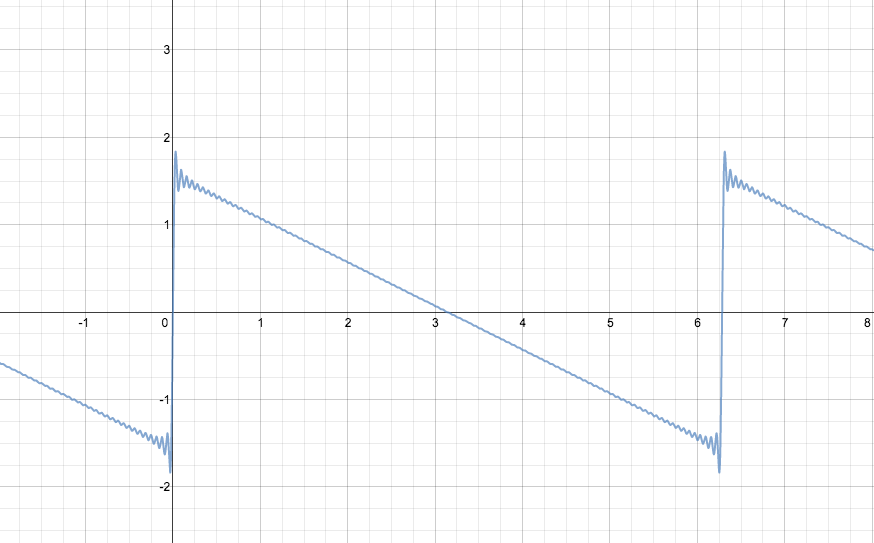
Thus the imaginary parts of the partial sums of $\sum \mathrm{e}^{inx}$ are always contained between $-\frac{1}{2}\tan\frac{x}{4}$ and $\frac{1}{2}\cot\frac{x}{4}$. To complete the picture, let's look at the real parts. Here is the graph of $\sum_{n=0}^{50} \cos nx$:
Using similar arguments as before, we can show that the value of $\sum_{n=0}^m \cos nx$ always lies between $\frac{1}{2}-\frac{1}{2}\csc\frac{x}{2}$ and $\frac{1}{2}+\frac{1}{2}\csc\frac{x}{2}$.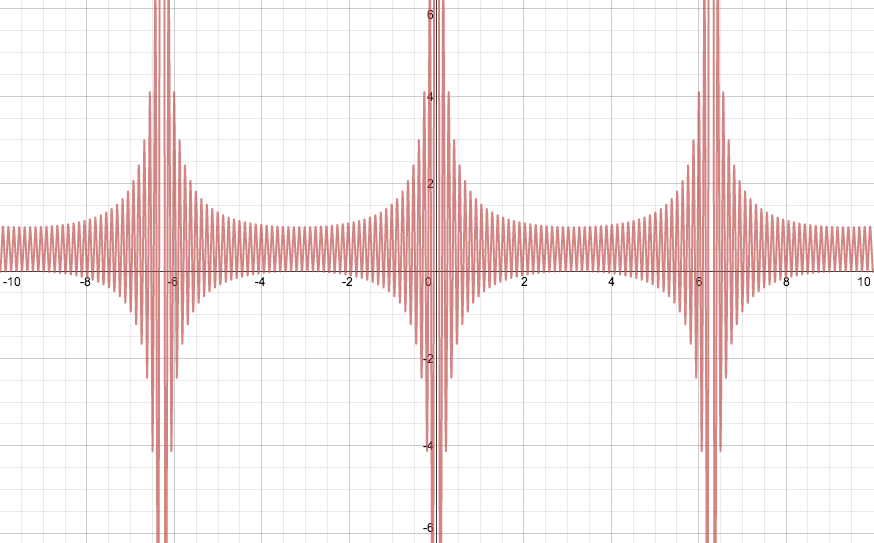
Therefore, even though the series $\sum z^n$ diverges whenever $|z| = 1$, the real and imaginary parts of its partial sums remain tightly constrained by values that depend analytically on the argument of $z$ (unless $z = 1$, i.e., its argument is a multiple of $2\pi$, in which case the series is just $1 + 1 + 1 + \cdots$).
Coda: The real and imaginary parts of $\sum \frac{z^n}{n^2}$ and $\sum \frac{z^n}{n}$ also look like Fourier series, no? Here, for instance, are the graphs of $\sum_{n=1}^{100}\frac{\cos nx}{n}$ (left) and $\sum_{n=1}^{100}\frac{\sin nx}{n}$ (right):
In particular, it looks like $\sum \frac{z^n}{n}$ diverges only when $z = 1$ (where it becomes the harmonic series). Can you find the functions to which its real and imaginary parts converge away from multiples of $2\pi$? Click on the graphs and try!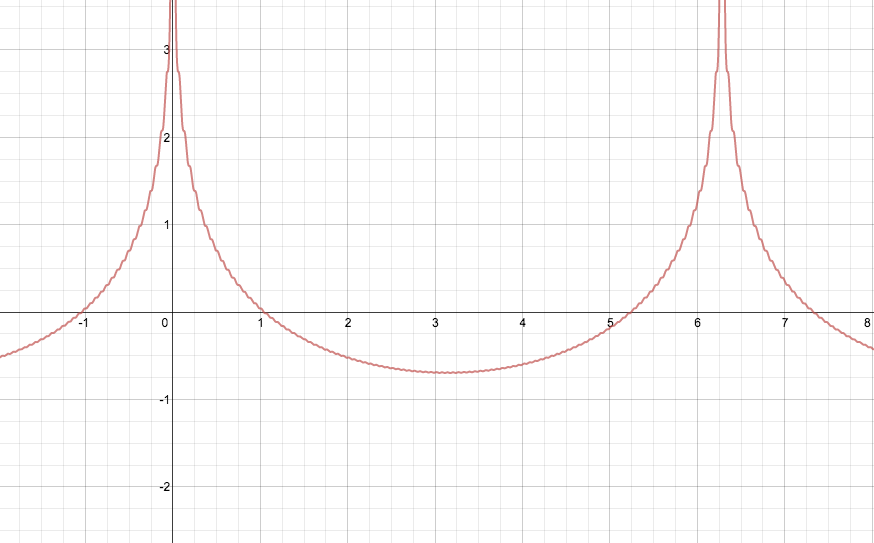
No comments:
Post a Comment